BitFunnel performance estimation

Hi! I’m going to talk about two things today.

First, I’m going to talk about one way to think about performance. That is, one way you can reason about performance.

Second, I’m going to talk about search. We’re going to look at search as a case study because, when talking about perfomance, it’s often useful to have something concrete to reason about. We could use any problem domain. However, I think that the algorithm we’re going to discuss today is particularly interesting because we use it in Bing, despite the fact that it’s in a class of algorithms that’s been considered obsolete for almost 20 years (at least as core search engine technology).

In case it’s not obvious, this is a psuedo-transcript of a talk given at StrangeLoop 2016. See this link if you’d rather watch the video. I wrote this up before watching my talk, so the text probably doesn’t match the video exactly.

BTW, when I say performance, I don’t just mean speed (latency), or speed (throughput). We could also be talking about other aspects of performance like power. Although our example is going to be throughput oriented, the same style of reasoning works for other types of performance.

Why do we care about performance? One is answer is that we usually don’t care because most applications are fast enough. That’s true! Most applications are fast enough. Spending unecessary time thinking about performance is often an error.

However, when applications get larger, most applications become performance sensitive! This happens both because making a large application faster reduces its cost, and also because making a large application faster can increase its revenue. The second part isn’t intuitive to many people, but we’ll talk more about that later.

How do we think about performance? It turns out that we can often reason about the performance with siple arithmetic. For many applications, even applications that take years to build, it’s possible to estimate the performance before building the system with simple back-of-the-envelope calculations.

Here’s a popular tweet. It has 500 retweets! “Working code attracts people who want to code. Design documents attract people who want to talk.”

I get it. Coding feels like real work. Meetings, writing docs, creating slide decks, and giving talks don’t feel like work.

But when I look at outcomes, well, I often see two applications designed to the same thing that were implemented with similar resources where one application is 10x or 100x faster than the other. And when I ask around and find out why, I almost inevetiably find that the team that wrote the faster application spent a lot of time on design. I tend to work on applications that take a year or two to build, so let’s say we’re talking about something that took a year and a half. For a project of that duration, it’s not uncommon to spend months in the design phase before anyone writes any code that’s intended to be production code. And when I look at the slower application, the team that created the slower appliction usually had the idea that “meetings and whiteboarding aren’t real work” and jumped straight into coding.

The problem is that if you have something that takes a year and a half to build, if you build it, measure the performance, and then decide to iterate, your iteration time is a year and a half, whereas on the whiteboard, it can be hours or days. Moreover, if you build a system without reasoning about what the performance should be, when you build the system and measure its performance, you’ll only know how fast it runs, not how fast it should run, so you won’t even know that you should iterate.

It’s common to hear advice like “don’t optimize early, just profile and then optimize the important parts after it works”. That’s fine advice for non-performance critical systems, but it’s very bad advice for performane critical systems, where you may find that you have to re-do the entire architecture to get as much performance out of the system as your machine can give you.

Before we talk about performance, let’s talk about scale. Because people often mean different things when they talk about scale, I’m going to be very concrete here.

Since we’re talking about search, let’s imagine a few representative corpus sizes we might want to search: ten thousand, ten million, and ten billion documents.

And let’s assume that each document is 5kB. If we’re talking about the web, that’s a bit too small, and if we’re talking about email, that’s a bit too big, but you can scale this number to whatever corpus size you have.

BTW, the specific problem we’re going to look at is: we have a corupus of documents that we want to be able to search, and we’re going to handle AND queries.

That is, queries of the form, I want this word, and this word, and this word. For example, I want the words large AND yellow AND dog. The systems we’ll look at today can handle ORs and NOTs, but those aren’t fundamentally different and talking about them will add complexity, so we’ll only look at AND queries.

First, let’s consider searching ten thousand documents at 5kB per doc.

If you want to get an idea of how big this is, you can think of this as email search (for one person) or forum search (for one forum) in a typical case.

a k times a k is a million, and five times time is fifty, so 5kB times ten thousand is 50MB.

50MB is really small!

Today, for $50, you can buy a phone off amazon that has 1GB of RAM. 50MB will easily fit in RAM, even on a low-end phone.

If our data set fits in RAM and we have 50MB, we can try the most naive thing possible and basially just grep through our data. If you want something more concrete, you can think of this as looping over all documents, and for each document, looping over all terms.

Since we only need to handle AND queries, we can keep track of all the terms we want, and if a document has all of the terms we want, we can add that to our list of matches.

Ok. So, for ten thousand documents, the most naive thing we can think of works. What about ten million documents?

If you want to get a feel for how big ten million documents, you can think of this is roughly wikipedia-sized. Today, English language wikipedia has about five million documents.

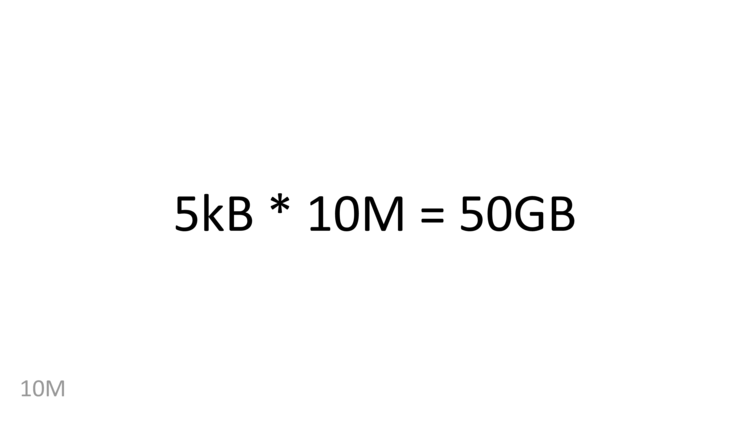
5kB times ten million is 50GB. This is really close to wikipedia’s size – today, wikipedia is a bit over 50GB (uncompressed articles in XML, no talk, no history).

We can’t fit that in RAM on a phone, and we’d need a pretty weird laptop to fit that in RAM on a laptop, but we can easily fit that in RAM on a low-budget server. Today, we can buy a $2000 server that has 128GB of RAM.

What happens when we try to run our naive grep-like algorithm? Well, our cheap server can get 25GB/s of bandwidth…

… and we have 50GB of data. That means that it takes two seconds to do one search query!

And while we’re doing a query, we’re using all the bandwidth on the machine, so we can’t expect to do anything else on the machine while queries are running, including other queries. This implies that it takes two seconds to do a query, or that we get one-half a query per second, or ¹⁄₂ QPS.

Is that ok? Is two seconds of latency ok? It depends.

For many applications, that’s totally fine! I know a lot of devs who have an internal search tool (often over things like logs) that takes a second or two to return results. They’d like to get results back faster, but given the cost/benefit tradeoff, it’s not worth optimizing things more.

How about ¹⁄₂ QPS? It depends.

As with latency, a lot of devs I know have a search service that’s only used internally. If you have 10 or 20 devs typing in queries at keyboards, it’s pretty unlikely that they’ll exceed ¹⁄₂ QPS with manual queries, so there’s no point in creating a system that can handle more throughput.

Our naive grep-like algorithm is totally fine for many search problems!

However, as services get larger, two seconds of latency can be a problem.

If we look at studies on latency and revenue, we can see a roughly linear relationship between latency and revenue over a pretty wide range of latencies.

Amazon found that every 100ms of latency cost them more than 1% of revenue. Google once found that adding 500ms of latency, or half a second, cost them 20% of their users.

This isn’t only true of large companies – when Mobify looked at this, they also found that 100ms of latency cost them more than 1% of revenue. For them, 1% was only $300k or so. But even though I say “only”, that’s enough to pay a junior developer for a year. Latency can really matter!

Here’s a query from some search engine. The result came back in a little over half a second. That includes the time it takes to register input on the local computer, figure out what to do with the input, send it across the internet, go into some set of servers somewhere, do some stuff, go back across the internet, come back into the local computer, do some more stuff, and then render the results.

That’s a lot of stuff! If you do budgeting for a service like this and you want queries to have a half-second end-user round-trip budget, you’ll probably only leave tens of milliseconds to handle document matching on the machines that recieve queries and tell you which documents matched the queries. Two seconds of latency is definitely not ok in that case.

Furthermore, for a service like Bing or Google, provisioning for ¹⁄₂ QPS is somewhat insufficient.

What we can do? Maybe we can try using an index instead of grepping through all documents.

If we use an index, we can get widely varying performance characteristics. Asking what the performance is like if we “use an index” is like asking what the performance is like if we “use an algorithm”. It depends on the algorithm!

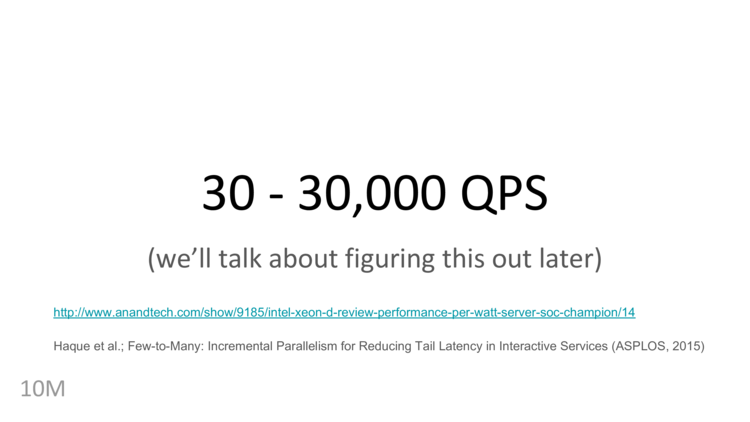
Today, we’ll talk about how to get performance in the range of thousands to tens of thousands of queries per second, but first…

… let’s finish our discussion about scale and talk about how to handle ten billion documents.

We’ve said that we can, using some kind of index, serve ten million documents from one machine with performance that we find to be acceptble. So how about ten billion?

With ten billion documents at 5kB a piece, we’re looking at 50TB. While it’s possible to get a single machine with 50TB of RAM, this approach isn’t cost effective for most problems, so we’ll look at using multiple cheap commodity machines instead of one big machine.

Search is a relatively easy problem to scale horizontally; that is, it’s relatively easy to split a search index across multiple machines. One way to do this (and this isn’t the only possible way) is to put different documents on different machines. Queries then go to all machines, and the result is just the union of all queries.

Since we have ten billion documents, and we’re assuming that we can serve ten million documents on a machine, if we split up the index we’ll have a thousand machines.

That’s ok, but if we have a cluster of a thousand machines and the cluster is in Redmond, and we have a customer in Europe, that could easily add 300ms of latnecy to the query. We’ve gone through all the effort of designing and index that can return a query in 10ms, and then we have customers that lose 300ms from having their queries go back and forth over the internet.

Instead of having a single cluster, we can use multiple clusters all over the world to reduce that problem.

Say we use ten clusters. Then we have ten thousand machines.

With ten thousand machines (or even with a thousand machines), we have another problem: given the failure rate of commodity hardware, with ten thousand machines, machines will be failing all the time. At any given time, in any given cluster, some machines will be down. If, for example, the machine that’s indexing cnn.com goes down and users who want to query that cluster can’t get results from CNN, that’s bad.

In order to avoid the loss of sites from failures, we might triple the number of machines for redundancy, which puts us at thirty thousand machines.

With thirty thousand machines, one problem we have is that we now have a distributed system. That’s a super interesting set of problems, but it’s beyond the scope of this talk.

Another problem we have is that we have a service that cost a non-trivial amount of money to run. If a machine costs a thousand dollars per year (amortized cost, including the cost of building out datacenters, buying machines, and running the machines), that puts us at thirty-million dollars a year. By the way, a thousand dollars a year is considered to be a relatively low total amortized cost. Even if we can hit that low number, we’re still looking at thirty-million dollars a year.

At thirty-million a year, if we can double the performance and halve the number of machines we need, that saves us fifteen-million a year. In fact, if we can even shave off one percent on the running time of a query, that would save three-hundred thousand dollars a year, saving enough money to pay a junior developer for an entire year.

Conventional wisdom often says that “machine time is cheaper than developer time, which means that you should use the most productive tools possible and not worry about performance”. That’s absolutely true for many applications. For example, that’s almost certainly true for any single-server rails app. But once you get to the point where you have thousands of machines per service, that logic is flipped on its head because machine time is more expensive than developer time.

Now that we’ve framed the discussion by talking about scale, let’s talk about search algorithms.

The problem we’re looking at is, given a bunch of documents, how can we handle AND queries.

The standard algorithm that people use for search indices is a posting list.

A posting list is basically what a layperson would call an index.

Here’s an index from the 1600s. If you look at the back of a book today, you’ll see the same thing: there’s a list of terms, and next to each term there’s a list pages that term appears on.

Computers don’t have pages in the same sense; if you want to imagine a simple version of a posting list, you can think of…

…a hash map from terms to linked lists of document ids. That is, a hash map where key is a term and the value is a list.

That’s one way to do it, and it’s standard. Another thing we could try to do is use Bloom Filters.

We do this in Bing in a system called BitFunnel. But before we can describe BitFunnel, we need to talk about how bloom filters work.

And before we talk about how bloom filters work, let’s consider a more naive solution we might construct.

One thing we might try would to be use something called in incidence matrix, that is, a 2d matrix where one dimension of the matrix is every single term we know about, and the other dimension is every single document we know about. Each entry in the matrix is a 1 if the term is in the document, and it’s a 0 if the term isn’t in the document.

What will the performance of that be?

Well, first, how many terms are there? How many terms do you think are on the internet? And let’s say we shard the internet a zillion ways and serve tens of millions of documents per server? How many unique terms do we have per server?

pause

someone shouts ten million

Turns out, when we do this, we can see tens of billions of terms per shard. This is often surprising to people. I’ve asked a lot of people this question, and people often guess that there are millons or billions of unique terms on the entire internet. But if you pick a random number under ten billion and search for it, you’re pretty likely to find it on the internet! So, there are probably more than ten billion terms on the internet!

In fact, if you limit the search to just github, you can find a single document with about fifty-million primes! And if you look at the whole internet, you can find a site with all primes under one trillion, which is over thirty-billion primes! If that site lands in a single shard, that shard is going to have at least thirty-billion unique terms. Turns out, a lot of people put long mathematical sequences online.

And in addition to numbers, there’s stuff that’s often designed to be unique, like catalog numbers, ID numbers, error codes, and GUIDs. Plus DNA! Really, DNA. Ok, DNA isn’t designed to be unique, but if you split it up into chunks of arbitrary numbers of characters, there’s a high probability that any N character chunk for N > 16 is unique.

There’s a lot of this stuff! One question you might ask is, do you need to index that stuff? Does anyone really search for GTGACCTTGGGCAAGTTACTTAACCTCTCTGTGCCTCAGTTTCCTCATCTGTAAAATGGGGATAATA?

It turns out, that when you ask people to evaluate a search engine, many of them will try to imagine the weirdest queries they can think of, try those, and then choose the search engine that handles those queries better. It doesn’t matter that they never do those queries normally. Some real people actually evaluate search engines that way. As a result, we have to index all of this weird stuff if we want people to use our search engine.

If we have tens of billions of terms, say we have thirty billion terms, how large is our incidence matrix? Even if we use a bit vector, one single document will take up thirty billion divided by 8 bytes, or 3.75GB. And that’s just one document!

How can we shrink that? Well, since most documents don’t contain most terms, we can hash terms down to a smaller space. Instead of reserving one slot for each unique term, we only need as many slots as we have terms in a document (times a constant factor which is necessary for bloom filter operation).

That’s basically what a bloom filter is! For the purposes of this talk, we can think of a bloom filter as a data structure that represents a set using a bit vector and a set of independant hash functions.

Here, we have the term “large” and we apply three independent hash functions, which hashes the term to locations five, seven, and twelve. Having three hash functions is arbitrary and we’ll talk about that tradeoff later.

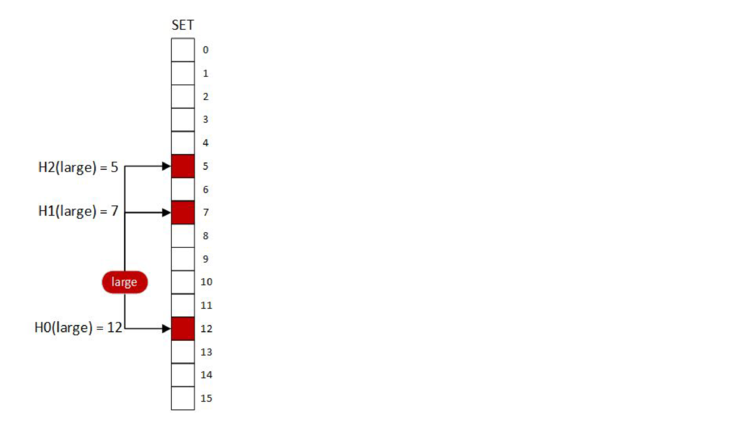
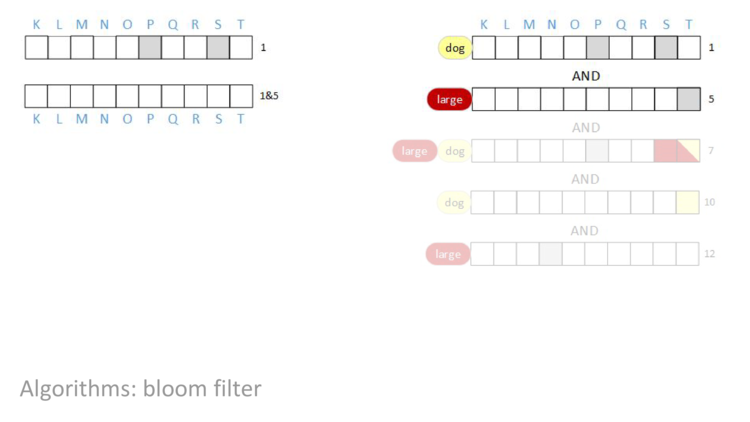
To insert “large” into the document, we’ll set bits five, seven, and twelve. To query for “large”, we’ll do the bitwise AND of those locations. That is, we’ll check to see if all three locations are 1. If any location is a 0, the result will be 0 (false) otherwise the result will be 1 (true). For any term we’ve inserted, the query will be 1 (true), because we’ve just set those bits.

In this series of diagrams, any bit that’s colored is a 1 and any bit that’s white is a 0. The red bits are associated with the term “large”.

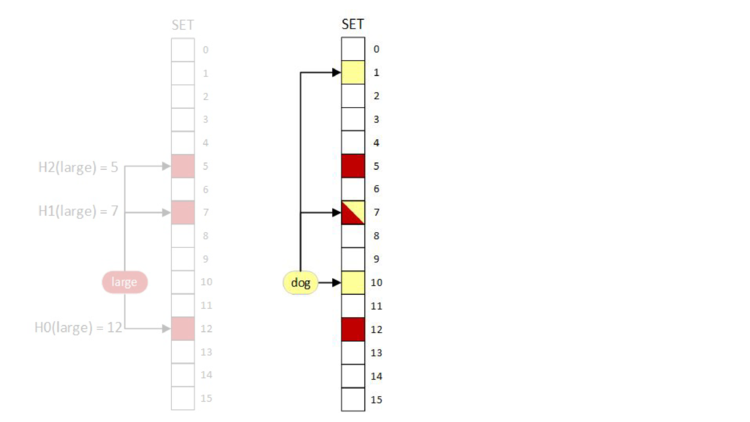
We can insert another term: “dog”. To do so, we’ll set those bits, one, seven, and ten. Seven was already set by “large” (red), but it’s fine to set it again with “dog”; all bits that are yellow are associated with the term “dog”. If we query for the term, as before, we’ll get a 1 (true) beacuse we’ve just set all the bits associated with the query.

We can also try querying a term that we didn’t insert into the document. Let’s say we query for “cat”, which happens to hash to three, ten, and twelve.

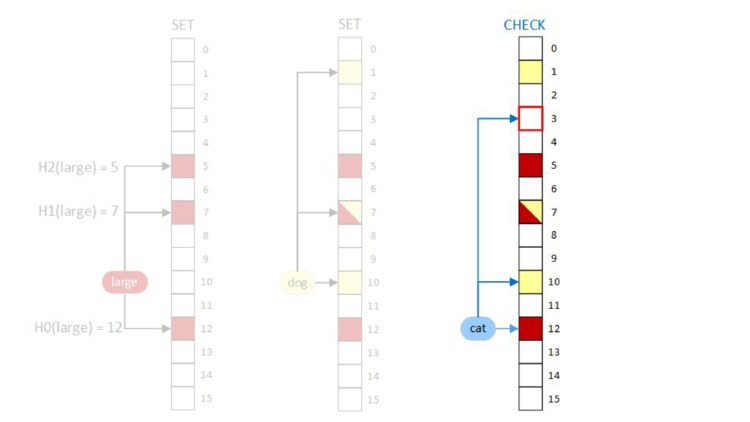
When we do the bitwise AND, we first look at bit three. Since bit three is a zero, we already know that the result will be 0 (false) before we look at the other bits and don’t have to look at bits ten and twelve.

Let’s try querying another term, “box”, and let’s say that term hashes to one, five, and ten.

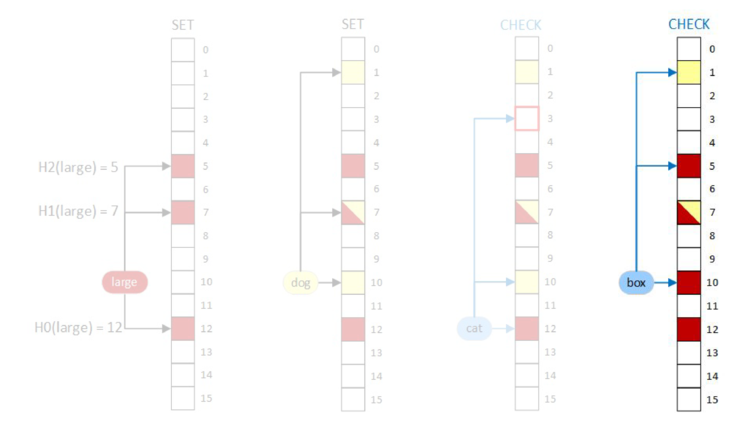
Even if we don’t insert this term into the document, the query shows that the term is in the document because those bits were set by other terms. We have a false positive!

How bad is this problem? Well, what’s the probability that any query will return a false positive?

Let’s assume we have ten percent bit density. This is something we can control – for example, if we have a bit vector of length 100, and we have ten terms, each of which is hashed to one location, we expect the bit density to be slightly less than 10%. It would be 10% if no terms hashed to the same location, but it’s possible that some terms might collide nd hash to the same location.

What’s the probability of a false positive if we hash to one location instead of three locations?

If the term is actually in the document, then we’ll set the bit, and if we do a query, since the bit was set, we’ll definitely return true, so there’s no probability of a false negative.

If the term isn’t in the document and we haven’t set the associated bit for this term because of this term, what’s the probability the bit is set? Because our bit desnity is .1, or 10%, the probability is 10%.

What if we hash to two locations instead of one location? Since we’re assuming we have uniform 10% bit density, we can multiply the probabilities: we get .1 * .1 = .01 = 1%.

For three locations, the math is the same as before: .1 * .1 * .1 = .001 = 0.1%.

As we hash to more locations, if we don’t increase the size of the bit vector, the bit density will go up. Same amount of space, set more bits, higher bit density. So we have to increase the number of bits, and we have to increase the number of bits linearly. As we increase the number of bits linearly, we get an exponential decrease in the probability of a false positive.

One intuition as to why bloom filters work is that we pay a linear cost and get an exponential benefit.

Ok. We’ve talked about how to use a bloom filter to represent one document. Since our index needs to represent multiple documents, we’ll use multiple bloom filters.

In this diagram, each of the ten columns represents a document. That is, we have documents A through J.

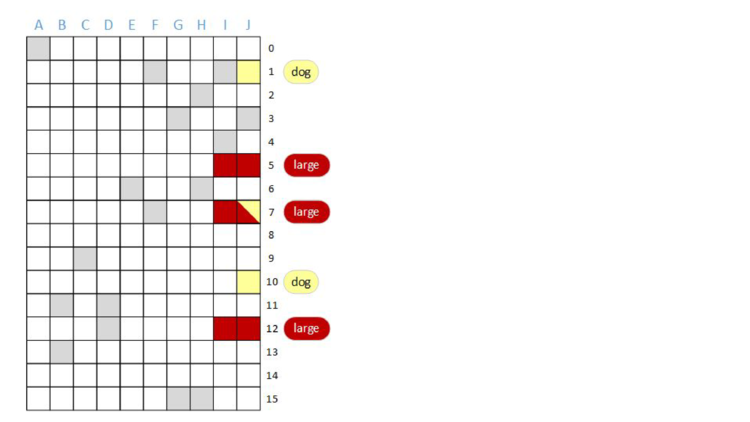
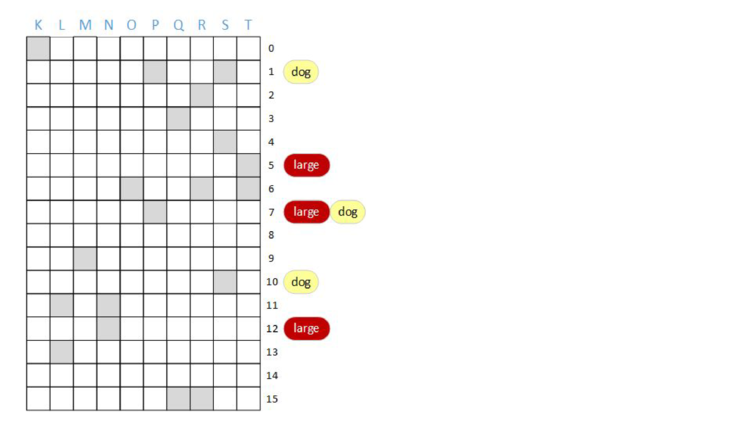
One thing we could do is have ten independent bloom filters. We know that we can have one bloom filter represent one document, so why not use ten bloom filters for ten documents?

If we’re going to do that, we might as well maintain the same mapping from terms to rows; that is, use the same hash functions for each column, so that when we do a query, we can do the query in parallel.

In the single-document example, when we did a query, we did the bitwise AND of some bits. Now, to do a query, we’ll do the bitwise AND of rows of bits.

Now we’re going to query for all documents that have both “large” AND “dog”. As before, bits that are red are associated with the term “large” and bits that are yellow are associated with the “dog”. Additionally, bits that are grey are associated with other terms.

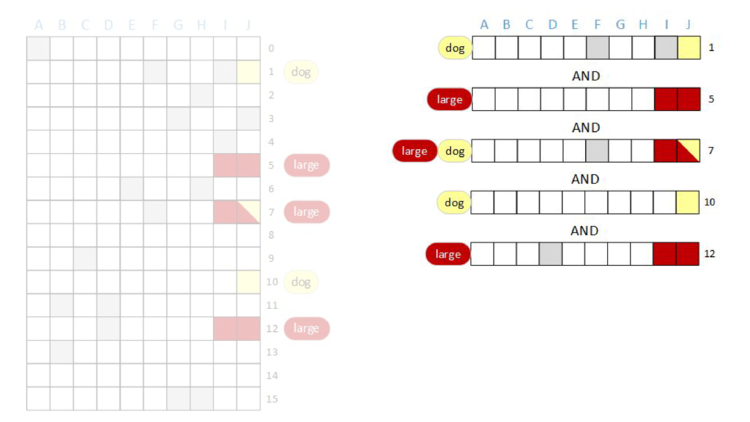
After we do the bitwise AND of all of the rows, the result will be a row vector with some bits set – those bits will be the documents that have both the terms “large” AND “dog”. We’re going to AND together rows one, five, seven, ten, and twelve and then look at the result.

In this diagram, on the right, the part’s that highlighted is the fraction of the query that we’ve done so far. On the left, the part’s that highlighted is the result of the computation so far.

When we start, we have row one.

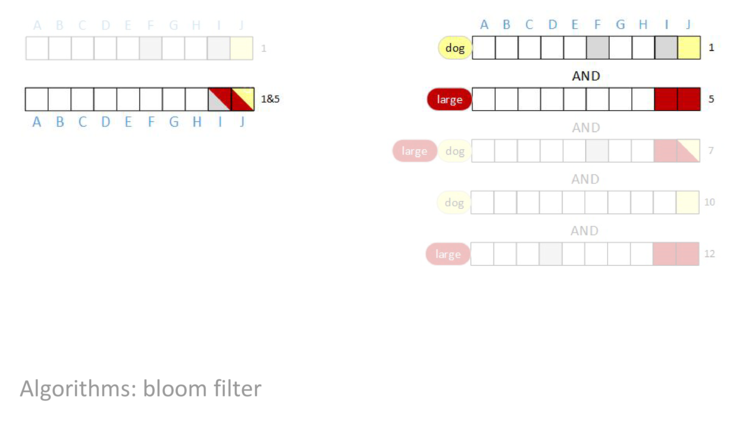
When we AND rows one and five together, we can see that bit F is cleared to zero.

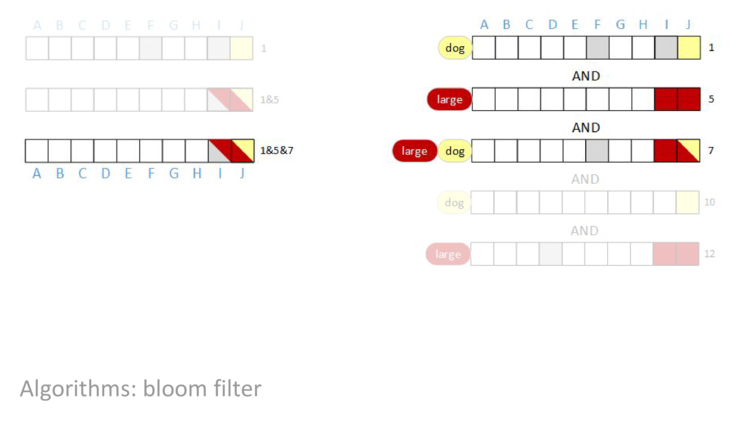
After we AND row seven into our result, nothing changes. Even though row seven has bit F set, an AND of a one and a zero is a zero, so the result in column F is still zero.

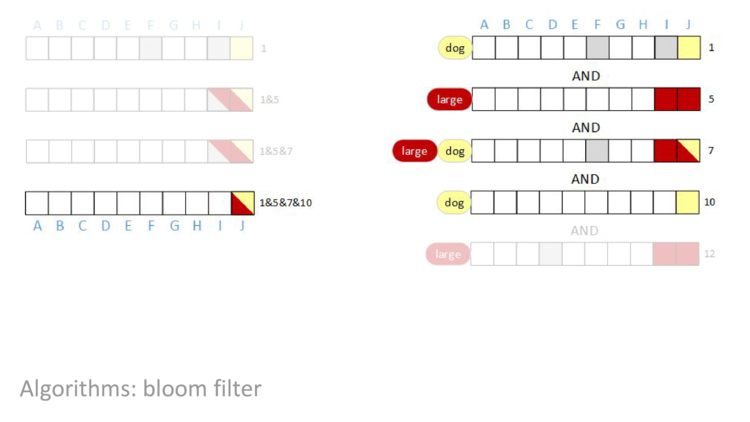
When we AND row ten in, bit I is cleared.

And then when we AND in the last row, nothing changes. The result of the query is that bit J is set. In other words, the query concludes that document J contains both the terms “large” AND “dog”, and no other document in this block contains both terms.

In our previous example, we queried a block of documents where at least one document contained both of the terms we cared about. We can also query a block of documents where none of the documents contain both of the terms.

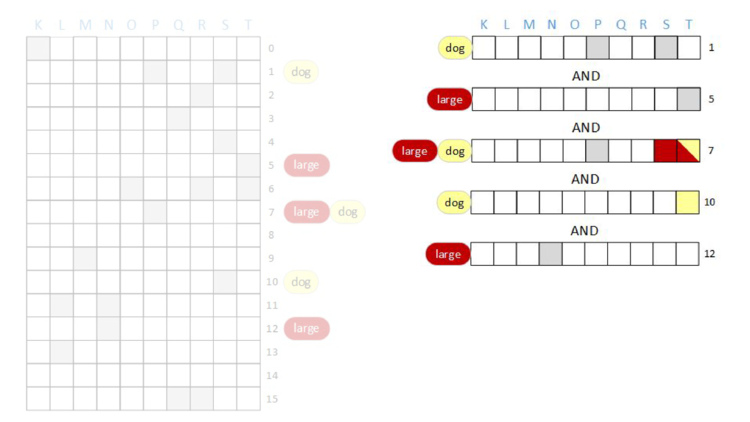
As before, we want to take the bitwise AND of rows one, five, seven, ten, and twelve.

And as before, we’ll start with row one.

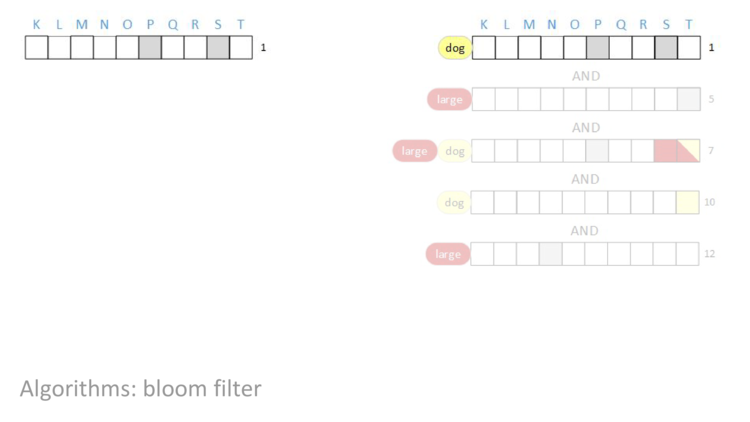
After we AND in row five, all of the bits are zero! When that happened in the “cat” example we did on a single document, we could stop because we knew that the document couldn’t possibly contain the term cat because we can’t set a bit by doing an AND. This same thing is true here, and we can stop and return that the result is all zeros.

I said, earlier, that we’d try to estimate the performance of a system. How do we do that?

We’ll want to have a cost model for operations and then figure out what operations we need to do. For us, we’re doing bitwise ANDs and reading data from memory. Reading data from memory is so much more expensive than a bitwise AND that we can ignore the cost of the ANDs and only consider the cost of memory accesses. If we had any disk accesses, those would even slower, but since we’re operating in memory, we’ll assume that a memory access is the most expensive thing that we do.

One bit of background is that on the machines that we run on, we do memory accesses in 512-bit blocks. So far, we’ve talked about doing operations on blocks of ten documents, but on the actual machine we can think of doing operations on 512 document blocks.

In that case, to get a performance estimate, we’ll need to know how many blocks we have, how many memory accesses (rows) we have per block, and how many memory accesses our machine can do per unit time.

To figure out how many memory accesses per block we want, we could work through the math…

…which is a series of probability calculations that will give us some number. I’m not going to do that here today, but it’s possible to do.

Another thing we can do is to run a simulation. Here’s the result of a simulation that was maybe thirty lines of code. This graph is a histogram of how many memory accesses we have to do per block, assuming we have 20% bit density, and a query that’s 14 rows.

If 14 rows sounds like a lot, well, we often do queries on 20 to 100 rows. That might sound weird, since we looked at an example where each term mapped to three rows. For one thing, terms can and sometimes do map to more than three rows. Additionally, we do query re-writing that makes queries more complicated (and hopefully better).

For example, let’s say we query for “large” AND “yellow” AND “dog”.

Maybe the user was actually searching for or trying to remember the name of some breed of large yellow dog, so we could re-write the query to be something like

(large AND yellow AND dog) OR (golden AND retriever)

as well as other breeds of dogs that can be large and yellow.

But the user might also be searching for some particular large yellow dog, so we could re-write the query to something like

(large AND yellow AND dog) OR (golden AND retriever) OR (old AND yeller)

and in fact we might want to query for the phrase “old yeller” and not just the AND of the terms, and so on and so forth.

When do you this kind of thing, and add in personalization based on location and query history, simple seeming queries can end up being relatively complicated, which is how we can get queries of 100 rows.

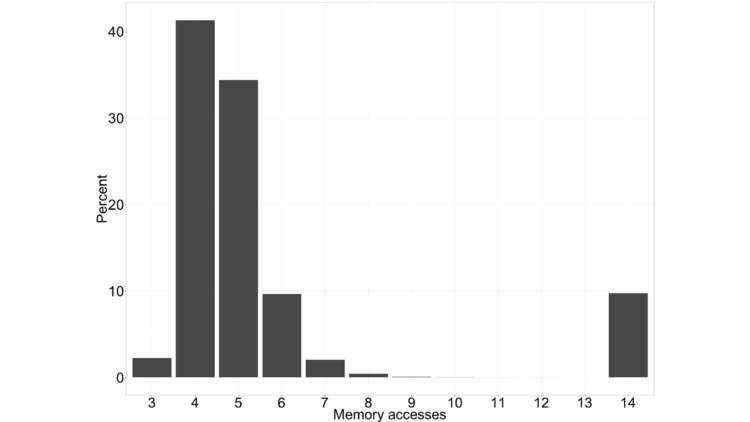
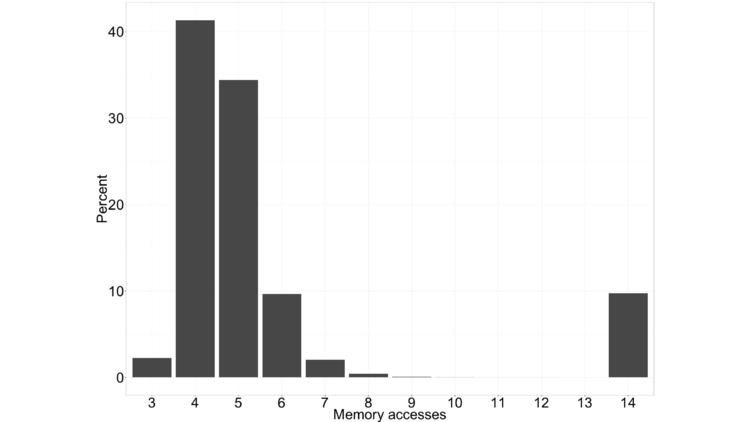
Coming back to the histogram of the number of memory accesses per block, we can see that it’s bimodal.

There’s he mode on the right, where we do 14 accesses. That mode corresponds to our first multi-document example, where at least one document in the block contained the terms. Because at least one document contained all of the terms, we don’t get all zeros in the result and do all 14 accesses.

The mode on the left, which is smeared out from 3 on to the right, is associated with blocks like our second example, where no document contained all of the terms in the query. In that case we’ll get a result of all zeros at some point with very high probability, and we can terminate the query early.

If we look at the average of the number of accesses we need for the left mode, it’s something like 4.6. On the right, it’s exactly 14. If we average these together, let’s say we get something like 5 accesses per query (just to get a nice, round, number).

Now we have what we need to do a first-order performance estimate!

If we go back to our roughly wikipedia-sized example, we had ten million documents. Since we’re on machine where memory accesses are 512 bits wide, that’s ten million divided by 512 equals twenty-thousand blocks, with a bit of rounding.

We said that we have roughly five memory accesses per query. If we have twenty-thousand blocks, that means that a query needs to do twenty-thousand times five memory accesses, or one hundred-thousand memory transfers.

We said that our cheap server can get 25GB/s of bandwidth out of. If we do 512-bit transfers, that’s three-hundred and ninety-million transfers per second.

If we divide three hundred-million transfers per second into a hundred thousand transfers per query, we get thirty-nine hundred QPS (with raounding from previous calculations).

When I do a calculation like this, if I’m just looking at the largest factors that affect performance, like we did here, I’m happy if we get within a factor of two.

If you adjust for a lot of smaller factors, it’s possible to get a more accurate estimate…

…but in the interest of time, we’re not going to look at all the smaller factors that add or remove 5% or 10% in performance.

However, there are a few major factors that affect performance a lot that I’ll briefly mention.

One thing is that our machines don’t only do document matching. So far, we’ve discussed an algorithm that, given a set of documents and a query will return a subset of those documents. We haven’t done any ranking, meaning that queries will come back unordered.

There are some domains where that’s fine, but in web search, we spend a significant fraction of CPU time ranking the documents that match the query.

Additionally, we also ingest new documents all the time. When news happens and people search for the news, they want to see it right away, so we can’t do batch updates.

This is something BitFunnel can actually do faster than querying. If we think about how queries worked, they’re global, in the sense that each query looked at information for each document. But when we’re ingesting new documents, since each document is a column, that’s possible to do without having to touch everything in the index. In fact, since our data structure is, in some sense, just an array that we want to set some bits in, it’s pretty straightforward to ingest documents with multiple threads while allowing queries with multiple threads.

It’s possible to work through the math for this the way we did for querying, but again, in the interest of time, I’ll just mention that this is possible.

Between ranking and ingestion, in the configuration we’re running today, that uses about half the machine, leaving half for matching, which reduces our performance by a factor of two.

However, we also have an optimization that drastically increases performance, which is using hierarchical bloom filters.

In our example, we had one bloom filter per document, which meant that if we had a query that only matched a single docucment, we’d have to examine at least one bit per document. In fact, we said that we’d end up looking at about five bits per document. If we use hierarchical bloom filters, it’s possible to look at a log number of bits per document instead of a linear number of bits per document.

The real production system we use has a number of not necessarily obvious changes in order to run at the speed that it does. Most of them aren’t required for the system to work correctly without taking up an unreasonable amount of memory, but one is.

If you take the algorithm I described it today and try to use it, when you look at sixteen rows in a block of ten documents, you might see something like this.

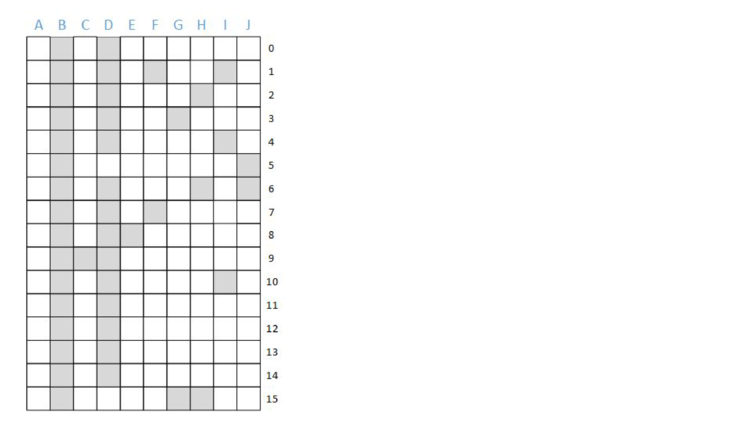
Notice that some columns (B and D) have most or all bits set, and some columns (A and C) have few or no bits set. This is because different documents have a different number of terms.

Let’s say we sized the number of rows so that we can efficiently store tweets. Let’s say, hypothetically, that means we need fifty rows. And then a weird document with ten million terms comes along and it wants to hash into the rows, say, thirty million times. That’s going to set every bit in its column, which means that every query will return true. Many weird documents like this contain terms that are almost never queried, so the query should almost never return true, but our system will always return true!

Say we size up the number of rows so that these weird ten million term documents are ok. Let’s say that means we need to have a hundred million rows. Ok, our queries will work fine, but we still have things like tweets that might want to set, say, sixteen bits. We said that we wanted to use bloom filters instead of arrays to save space by hashing to reduce the size of our array, but now we have all of these really sparse columns that have something like sixteen out of a hundred million bits set.

To get around this problem, we shard (split up the index) by the number of terms per document. Unlike many systems, which only run in a sharded configuration when they need to spill over onto another machine, we always run in a sharded configuration, even when we’re running on a single machine.

Although there are other low level details that you’d want to know to run an efficient system, this is the only change that you absolustely have to take into account when compared to the algorithm I’ve described today.

Let’s sum up what we’ve look at today.

Before we talk about the real conclusions, let’s discuss a few false impressions this talk could give.

“Search is simple”.

You’ve seen me describe an algorithm that’s used in production for web search. The algorithm is simple enough that it could be described in a thirty-minute talk with no background. However, to run this algorithm at the speed we’ve estimated today, there’s a fair amount of low-level implementation work. For example, to reduce the (otherwise substantial) control flow overhead of querying and ranking, we compile both our queries and our query ranking.

Additionally, even if this system were simple, this is less than 1% of the code in Bing. Search has a lot of moving parts and this is just one of them.

“Bloom filters are better than posting lists”.

I went into some detail about bloom filters and didn’t talk about posting lists much, except to say that they’re standard. This might give the impression that bloom filters are categorically better than posting lists. That’s not true! I only didn’t describe posting lists in detail and do a comparison because state-of-the-art posting list implementations are tremendously complicated and I couldn’t describe them to a non-specialist audience in thirty minutes, let alone do the comparison.

If you do the comparison, you’ll find that when one is better than the other depends on your workload. For an argument that posting lists are superior to bloom filters, see Zobel et al., “Inverted files versus signature files for text indexing”.

“You can easily reason about all performance”.

Today, we look at how an algorithm worked and estimated the performance of a system that took years to build. This was relatively straightforward because we were trying to calculate the average throughput of a system, which is something that’s amenable to back-of-the-envelope math. Something else that’s possible, but slightly more difficult, is to estimate the latency of a query on an unloaded system.

Something that’s substantially harder is estimating the latency on a system as load varies, and estimating the latency distribution.

Ok, now for an actual conclusion.

You can often reason about performance…

…and you can do so with simple arithmetic. Today, all we did was multiply and divide. Sometimes you might have to add, but you can often guess what the performance of a system should be with simple calculations.

Thanks to all of these people for help with this talk! Also, I seem to have forgotten to put Bill Barnes on the list, but he gave me some great feedback!

Post original talk: also, thanks to Laura Lindzey, Larry Marbuger, and someone’s name who I can’t remember for giving me great post-talk feedback that changed how I’m giving the next talk.

If you want to read more about the index we talked about today, BitFunnel, you can get more information at bitfunnel.org. We also have some code up at github.com/bitfunnel/bitfunnel.

Oh, yeah, I’m told you have to introduce yourself at these things. I’m Dan Luu, and I have a blog at danluu.com where I blog about the kind of thing I talked about here today. That is, I often write about performance, algorithms and data structures, and tradeoffs between different techniques.

Thanks for your time. Oh, also, I’m not going to take questions from the stage because I don’t know how people who aren’t particularly interested in the questions often feel obligated to stay for the question period. However, I really enjoy talking about this stuff and I’d be happy to take questions in the hallway or anytime later.